
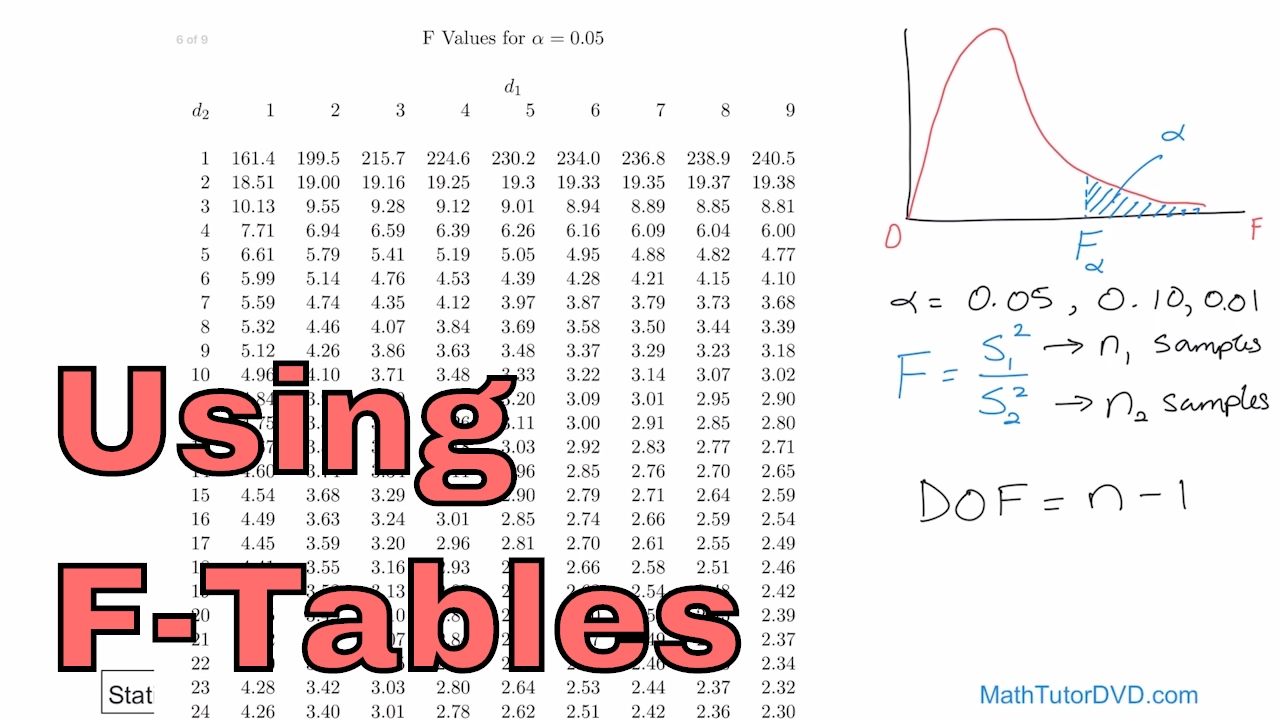
A simple test: Do these two samples come from populations with the same variance?īecause the F-distribution is generated by drawing two samples from the same normal population, it can be used to test the hypothesis that two samples come from populations with the same variance. The second is one-way analysis of variance (ANOVA), which uses the F-distribution to test to see if three or more samples come from populations with the same mean. The first is a very simple test to see if two samples come from populations with the same variance. There are two uses of the F-distribution that will be discussed in this chapter. Since F goes from zero to very large, with most of the values around one, it is obviously not symmetric there is a long tail to the right, and a steep descent to zero on the left. It is equally possible for s 2 2 to be a lot larger than s 1 2, and then F would be very close to zero. If s 1 2 is a lot larger than s 2 2, F can be quite large. Thinking about ratios requires some care. All of the F-scores will be positive since variances are always positive - the numerator in the formula is the sum of squares, so it will be positive, the denominator is the sample size minus one, which will also be positive. If s 1 2 and s 2 2 come from samples from the same population, then if many pairs of samples were taken and F-scores computed, most of those F-scores would be close to one. Think about the shape that the F-distribution will have. Because we know that sampling distributions of the ratio of variances follow a known distribution, we can conduct hypothesis tests using the ratio of variances. Not surprisingly, over the intervening years, statisticians have found that the ratio of sample variances collected in a number of different ways follow this same distribution, the F-distribution. Years ago, statisticians discovered that when pairs of samples are taken from a normal population, the ratios of the variances of the samples in each pair will always follow the same distribution. The procedure fails to reject the hypotheses that the other group means are different from each other.Chapter 6. The p-value of 0.0292 indicates that the mean bacteria counts in the milk from the fourth shipment is different from the ones from the fifth. The p-values 0.0059, 0.0013, and 0.0001 indicate that the mean bacteria counts in the milk from the first shipment is different from the ones from the second, third, and fourth shipments. The last column shows the p-values for the tests. For example, the first row compares the means for groups 1 and 2. The first two columns show which group means are compared with each other. Group A Group B Lower Limit A-B Upper Limit P-value You can provide sample data as a vector or a matrix. That checks for normality: the Anderson-Darling test ( adtest), the chi-squared goodness of fit You can check the normality assumption visuallyĪlternatively, you can use one of the Statistics and Machine Learning Toolbox™ functions It is known to be robust to modest violations In this case, each group or column can have a different number of observationsĪNOVA is based on the assumption that all sample populationsĪre normally distributed. In group, for the data in vector or matrix y. Same number of observations (i.e., a balanced design).Īnova1(y,group) tests the equality of group means, specified In matrix y, where each column is a different group and has the = α k) against the alternative hypothesis that at least one group isĭifferent from the others ( H 1 : α i ≠ α j for at least one i and j).Īnova1(y) tests the equality of column means for the data The model assumes that the columns of y are theĪNOVA helps determine if the constants are all the same.ĪNOVA tests the hypothesis that all group means are equal ( H 0 : α 1 = α 2 =. This model is also called the means model. Mean and constant variance, i.e., ε i j ~ The random error, independent and normally distributed, with zero The population mean for the jth group (level or Number, and j represents a different group (level) of the Is an observation, in which i represents the observation


 0 kommentar(er)
0 kommentar(er)
